
Implementation of Friction:
Within this project, I implemented a custom, 2D physics system complete with friction. The simulation contains 3 basic shapes: planes, cubes & spheres. Elasticity is the force that causes two objects to bonce away from each other upon colliding. This force acts along the collision normal, being a normalized vector between the two colliding points at its simplest. The force is then distributed between the two bodies based on their mass relative to each other with greater masses gaining less acceleration from the collision.
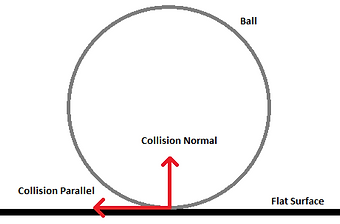
Friction is the fun one. It acts along, what I call, the collision parallel. The collision parallel is a perpendicular vector to the collision normal but in the same direction as the combined velocity of the two colliding points. As the system is 2D, we can cheat this by rotating the collision normal 90 degrees.
Now, friction follows 2 basic rules:
-
Any 2 colliding points want to have a velocity sum of 0.
-
A stationary body will use a different friction factor than a moving body.
Step 1: Calculating Friction
For rule 1, friction wants to do the least work possible to achieve this goal. Rule 2, will cause 2 colliding points to eventually comply to rule 1. Stationary friction factor is almost always greater than moving friction factor. Friction factor is basically what defines how slippery a surface is. It ranges from 0, no friction, to 1, max friction.
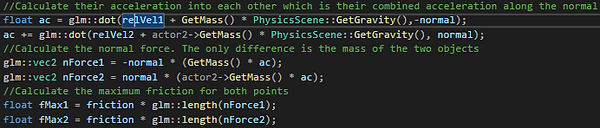
When two points collide, we apply friction first, then elasticity. The first job is to calculate the average friction factor to determine how slippery the collision it and the combined velocity of the two points. From this, we calculate the maximum friction we can apply, to avoid jittery motion.
From this data, we can calculate their acceleration into each other and thus, their individual normal force. The normal force is mass * acceleration, it’s the force that holds you onto an object. If you are sitting down, its gravity * your mass, if you are holding paper against a wall, it’s the force of you pushing the paper onto the wall to stop it falling. We use this value to calculate the maximum force each individual point can have applied to it.
Now, we get the ratio between the two masses. The ratio should be between 0 – 1 so we need to check which mass is larger and adjust the calculations respectively. Earlier, we calculated the change in velocity along the collision parallel. We take that value and divide it by 2. This new value, fForce represents how much velocity each point needs to lose if they have equal mass. Now we calculate how much force each point is to take. For the point with the least mass, the calculation is fForce * (1 + (1 - ratio)) to put it into 1 – 2 range and the greater mass is (fForce * ratio). This is to account for the friction division earlier when calculating fForce. Funnily enough, fForce is actually pure velocity/acceleration. As such, we need to apply their own respective masses to get the force to apply.

Step 2: Pivoting
Finally, we just figure out which direction to apply the friction forces in to make sure the objects spin the correct way . Now, if you thought we were done, you’d almost be right. Before we apply the friction forces we need to do something a bit hacky. For an object, such as a box, if it were to land on one of its corners, on a flat surface with 100% or even 10000% friction, rather than pivoting on that corner and falling on its side, the corner will slip out from under the cube and it will land flat.

As such, when applying the friction force, we need to adjust the velocity of the CoM so that it pivots on the point. So before we apply the force to make the object rotate, we need to directly manipulate their velocity.
Now we treat everything like a sphere. We start off by getting: The “distance” from the center of mass to the contact points, local to each object. The “force” of the center of mass (CoM). Velocity * Mass. And the moment of the point. Mass * distance^2. Now we calculate the torque, using the local contact point for the respective objects for both the angle and radius and the “force” of the CoM.
Finally, if the torque is not 0, we calculate the velocity of the object too, Torque / Point Moment * Local Contact rotated 90 degrees clockwise but we don’t apply it. Just before applying it, we get the difference between the current and final velocity and scale it by the friction factor. This ensures that the body moves relative to how slippery the surface is. If the friction factor is 0, there will be no pivot as the CoM gets no velocity, 0.5 and the body will pivot a bit but the corner will still slip out and 1 will result in a full pivot. And we repeat for the second object in the collision. And now the CoM will move! Now if a rotating box lands on a corner, it will pivot on that corner!

And now we apply the friction force we calculated earlier, and do elasticity. With all that, we end up with what you see below. Now, this isn't a perfect implementation, mostly because of the pivoting code. Normally, the mass behind the contact point would reduce as the box pivots, later causing the contact point to slip. I hope you are still here after that because there’s more cool stuff to look at & read about!